数据库事务隔离发展历史

事务隔离是数据库系统设计中根本的组成部分，本文主要从标准层面来讨论隔离级别的发展历史，首先明确隔离级别划分的目标；之后概述其否定之否定的发展历程；进而引出 Adya给出的比较合理的隔离级别定义，最终总结隔离标准一路走来的思路。

目标

事务隔离是事务并发产生的直接需求，最直观的、保证正确性的隔离方式，显然是让并发的事务依次执行，或是看起来像是依次执行。但在真实的场景中，有时并不需要如此高的正确性保证，因此希望牺牲一些正确性来提高整体性能。通过区别不同强度的隔离级别使得使用者可以在正确性和性能上自由权衡。随着数据库产品数量以及使用场景的膨胀，带来了各种隔离级别选择的混乱，数据库的众多设计者和使用者亟需一个对隔离级别划分的共识，这就是标准出现的意义。一个好的隔离级别定义有如下两个重要的目标：

• 正确：每个级别的定义，应该能够将所有损害该级别想要保证的正确性的情况排除在外。也就是说，只要实现满足某一隔离级别定义，就一定能获得对应的正确性保证。
• 实现无关：常见的并发控制的实现方式包括，锁、OCC以及多版本 。而一个好的标准不应该限制其实现方式。

ANSI SQL标准(1992)：基于异象

1992年ANSI首先尝试指定统一的隔离级别标准，其定义了不同级别的异象(phenomenas)， 并依据能避免多少异象来划分隔离标准。异象包括：

• 脏读（Dirty Read）: 读到了其他事务还未提交的数据；
• 不可重复读（Non-Repeatable/Fuzzy Read）：由于其他事务的修改或删除，对某数据的两次读取结果不同；
• 幻读（Phantom Read）：由于其他事务的修改，增加或删除，导致Range的结果失效（如where 条件查询）。

通过阻止不同的异象发生，得到了四种不同级别的隔离标准：

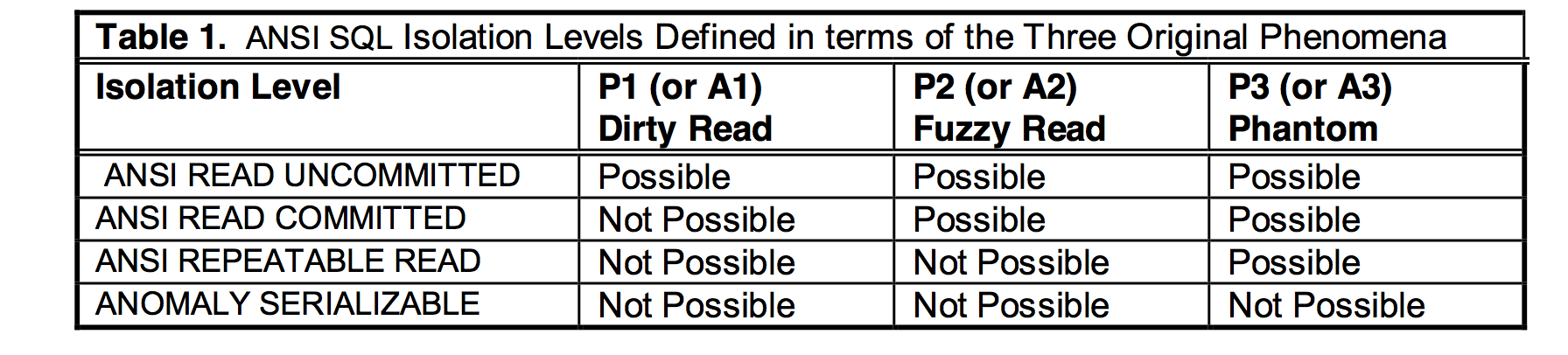ANSI SQL标准看起来是非常直观的划分方式，不想要什么就排除什么，并且做到了实现无关。然而，现实并不像想象美好。因为它并不正确。

A Critique of ANSI(1995)：基于锁

几年后，微软的研究员们在A Critique of ANSI SQL Isolation Levels一文中对ANSI的标准进行了批判，指出其存在两个致命的问题：

1，不完整，缺少对Dirty Write的排除

ANSI SQL标准中所有的隔离级别都没有将Dirty Write这种异象排除在外，所谓Dirty Write指的是两个未提交的事务先后对同一个对象进行了修改。而Dirty Write之所以是一种异象，主要因为他会导致下面的一致性问题：

H0: w1[x] w2[x] w2[y] c2 w1[y] c1

这段历史中，假设有相关性约束x=y，T1尝试将二者都修改为1，T2尝试将二者都修改为2，顺序执行的结果应该是二者都为1或者都为2，但由于Dirty Write的发生，最终结果变为x=2，y=1，不一致。

2，歧义

ANSI SQL的英文表述有歧义。以Phantom为例，如下图历史H3：

H3：r1[P] w2[insert y to P] r2[z] w2[z] c2 r1[z] c1

假设T1根据条件P查询所有的雇员列表，之后T2增加了一个雇员并增加了雇员人数值z，之后T1读取雇员人数z，最终T1的列表中的人数比z少，不一致。但T1并没有在T2修改链表后再使用P中的值，是否就不属于ANSI中对Phantom的定义了呢？这也导致了对ANSI的表述可能有严格和宽松两种解读。对于Read Dirty和Non-Repeatable/Fuzzy Read也有同样的问题。

那么，如何解决上述两个问题呢？Critique of ANSI的答案是：宁可错杀三千，不可放过一个，即给ANSI标准中的异象最严格的定义。Critique of ANSI改造了异象的定义：

P0: w1[x]…w2[x]…(c1 or a1) (Dirty Write)

P1: w1[x]…r2[x]…(c1 or a1) (Dirty Read)

P2: r1[x]…w2[x]…(c1 or a1) (Fuzzy or Non-Repeatable Read)

P3: r1[P]…w2[y in P]…(c1 or a1) (Phantom)

此时定义已经很严格了，直接阻止了对应的读写组合顺序。仔细可以看出，此时得到的其实就是基于锁的定义:

• Read Uncommitted，阻止P0：整个事务阶段对x加长写锁
• Read Commited，阻止P0，P1：短读锁 + 长写锁
• Repeatable Read，阻止P0，P1，P2：长读锁 + 短谓词锁 + 长写锁
• Serializable，阻止P0，P1，P2，P3：长读锁 + 长谓词锁 + 长写锁

问题本质

可以看出，这种方式的隔离性定义保证了正确性，但却产生了依赖实现方式的问题：太过严格的隔离性定义，阻止了Optimize或Multi-version的实现方式中的一些正常的情况：

• 针对P0：Optimize的实现方式可能会让多个事务各自写自己的本地副本，提交的时候只要顺序合适是可以成功的，只在需要的时候才abort，但这种选择被P0阻止；
• 针对P2：只要T1没有在读x，后续没有与x相关的操作，且先于T2提交。在Optimize的实现中是可以接受的，却被P2阻止。

回忆Critique of ANSI中指出的ANSI标准问题，包括Dirty Write和歧义，其实都是由于多Object之间有相互约束关系导致的，如下图所示，图中黑色部分表示的是ANSI中针对某一个异象描述的异常情况，灰色部分由于多Object约束导致的异常部分，但这部分在传统的异象定义方式中并不能描述，因此其只能退而求其次，扩大限制的范围到黄色部分，从而限制了正常的情况。：

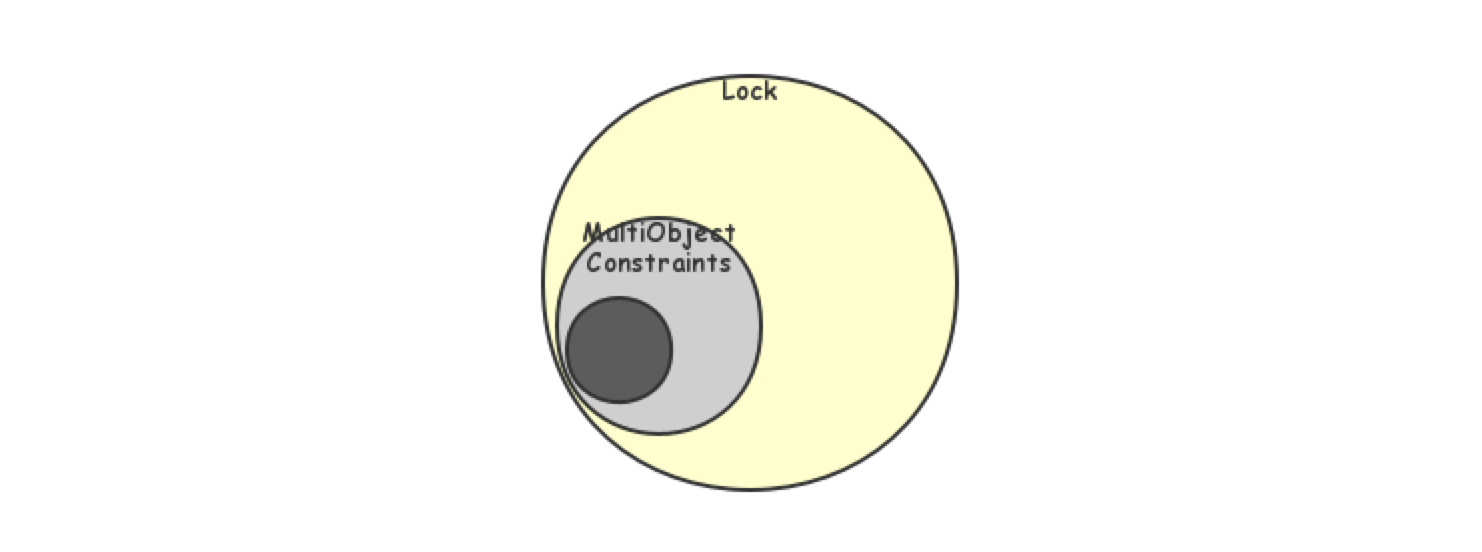
由此，可以看出问题的本质：由于异象的描述只针对单个object，缺少描述多object之间的约束关系，导致需要用锁的方式来作出超出必须的限制。相应地，解决问题的关键：要有新的定义异象的模型，使之能精准的描述多object之间的约束关系，从而使得我们能够精准地限制上述灰色部分，而将黄色的部分解放出来。Adya给出的答案是序列化图。

A Generalized Theory(1999)：基于序列化图

Adya在Weak Consistency: A Generalized Theory and Optimistic Implementations for Distributed Transactions中给出了基于序列化图得定义，思路为先定义冲突关系；并以冲突关系为有向边形成序列化图；再以图中的环类型定义不同的异象；最后通过阻止不同的异象来定义隔离级别。

序列化图（Direct Serialization Graph, DSG）

序列化图是用有向图的方式来表示事务相互之间的依赖关系，图中每个节点表示一个事务，有向边表示存在一种依赖关系，事务需要等到所有指向其的事务先行提交，如下图所示历史的合法的提交顺序应该为：T1，T2，T3：

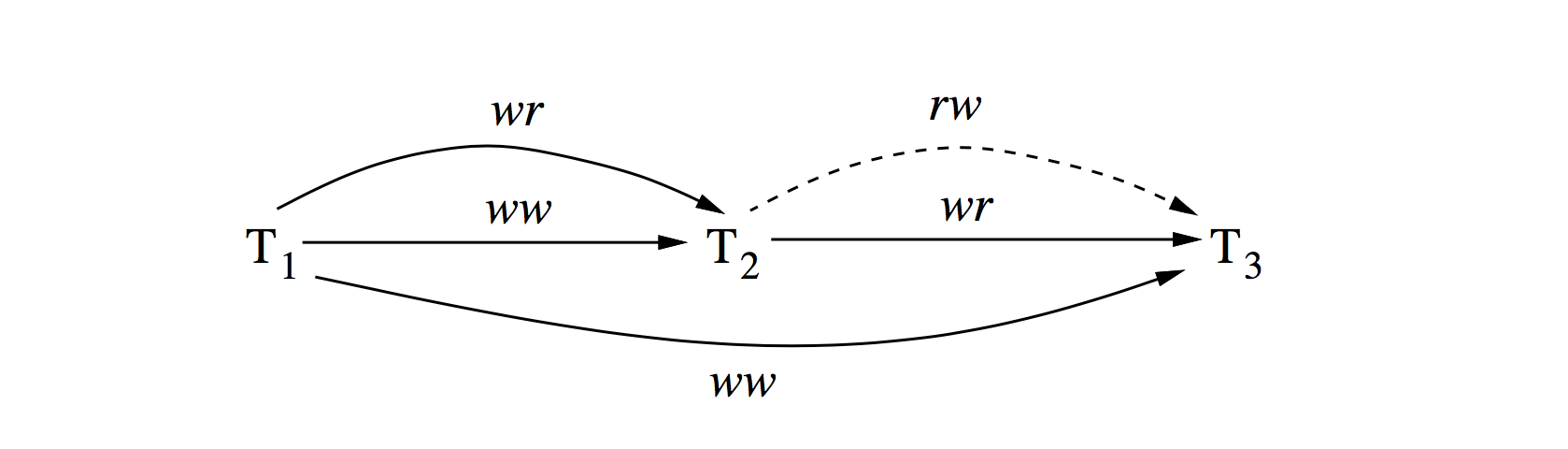
这里的有向边包括三种情况：

• 写写冲突ww（Directly Write-Depends）：表示两个事务先后修改同一个数据库Object(w1[x]…w2[x]…)；
• 先写后读冲突wr（Directly Read-Depends）：一个事务修改某个数据库Object后，另一个对该Object进行读操作（w1[x]…r2[x]…）；
• 先读后写冲突rw（Directly Anti-Depends）：一个事务读取某个Object或者某个Range后，另一个事务进行了修改（r1[x]…w2[x]… or r1[P]…w2[y in P]）；

基于序列化图的异象定义：

根据有向图的定义，我们可以将事务对不同Object的依赖关系表示到一张同一张图中，而所谓异象就是在图中找不到一个正确的序列化顺序，即存在某种环。而这种基于环的定义其实就是将基于Lock定义的异象最小化到图中灰色部分：

1，P0(Dirty Write) 最小化为 G0(Write Cycles)：序列化图中包含两条边都为ww冲突组成的环，如H0：

H0: w1[x] w2[x] w2[y] c2 w1[y] c1

可以看出T1在x上与T2写写冲突，T2又在y上与T1写写冲突，形成了如下图所示的环。

2，P1(Dirty Read) 最小化为 G1：Dirty Read异象的最小集包括三个部分G1a(Aborted Reads)，读到的uncommitted数据最终被abort；G1b(Intermediate Reads) ：读到其他事务中间版本的数据；以及G1c(Circular Information Flow)：DSG中包含ww冲突和wr冲突形成的环。

3，P2(Fuzzy or Non-Repeatable Read) 最小化为 G2-item(Item Anti-dependency Cycles) ：DSG中包含环，且其中至少有一条关于某个object的rw冲突

4，P3(Phantom) 最小化为 G2(Anti-dependency Cycles): DSG中包含环，并且其中至少有一条是rw冲突，仍然以上面的H3为例：

H3：r1[P] w2[insert y to P] r2[z] w2[z] c2 r1[z] c1

T1在谓词P上与T2 rw冲突，反过来T2又在z上与T1wr冲突，如下图所示：

对应的隔离级别：

通过上面的讨论可以看出，通过环的方式我们成功最小化了异象的限制范围，那么排除这些异象就得到了更宽松的，通用的隔离级别定义：

• PL-1（Read Uncommitted）：阻止G0
• PL-2（Read Commited）：阻止G1
• PL-2.99（Repeatable Read）：阻止G1，G2-item
• PL-3（Serializable）：阻止G1，G2

其他隔离级别：

除了上述的隔离级别外，在正确性的频谱中还有着大量空白，也就存在着各种其他隔离级别的空间，商业数据库的实现中有两个比较常见：

1，Cursor Stability

该隔离界别介于Read Committed和Repeatable Read之间，通过对游标加锁而不是对object加读锁的方式避免了Lost Write异象。

2， Snapshot Ioslation

事务开始的时候拿一个Start-Timestamp的snapshot，所有的操作都在这个snapshot上做，当commit的时候拿Commit-Timestamp，检查所有有冲突的值不能再[Start- Timestamp, Commit-Timestamp]被提交，否则abort。长久以来，Snapshot Ioslation一直被认为是Serializable，但其实Snapshot Ioslation下还会出现Write Skew的异象。之后的文章会详细介绍如何从Snapshot Ioslation出发获得Serializable。

总结

对于事务隔离级别的标准，数据库的前辈们进行了长久的探索：

• ANSI isolation levels定义了异象标准，并根据所排除的异象，定义了，Read Uncommitted、Read Committed、Repeatable Read、Serializable四个隔离级别；
• A Critique of ANSI SQL Isolation Levels认为ANSI的定义并没将有多object约束的异象排除在外，并选择用更严格的基于Lock的定义扩大了每个级别限制的范围；
• Weak Consistency: A Generalized Theory and Optimistic Implementations for Distributed Transactions认为基于Lock的定义过多的扩大了限制的范围，导致正常情况被排除在外，从而限制了Optimize类型并行控制的使用；指出解决该问题的关键是要有模型能准确地描述这种多Object约束；并给出了基于序列化图的定义方式，将每个级别限制的范围最小化。

参考

A History of Transaction Histories

ANSI isolation levels

A Critique of ANSI SQL Isolation Levels

Weak Consistency: A Generalized Theory and Optimistic Implementations for Distributed Transactions

Generalized Isolation Level Definitions